The semester Advanced Software Development (ASD for short) had an assignment which requires me to write a blog about me exploring a new programming paradigm besides the typical one thought at school (object-oriented).
We had the choice of picking one of the following five languages: Prolog, Scala, Erlang, Clojure and Haskell. Last year I picked Haskell with its functional programming paradigm, but due to time constraints, I couldn’t finish the assignment in time. Instead of trying something I’ve already done once, I thought I should pick something different and see what the other languages are like. Thus, I decided that this time around, I would look into Prolog.
The assignment consisted of three parts:
- Picking a language and paradigm (already done that)
- Writing (IT) blog posts about my experiences and opinions related to this selected language and paradigm, while working my way through the Prolog chapter in the book “Seven Languages in Seven Weeks” by Bruce A. Tate (referred to as “the book” from now on). Conveniently enough, I already have this blog in a rather unknown corner of the internet I can use. At times, I will also try to compare various features of the language with the programming languages and paradigms I already know.
- Defining a challenge befitting the selected language and paradigm and blogging my hardships and problems along with it.
Prolog
Prolog is a logic programming language. Various resources on the internet mention that it’s good for Natural Language Processing and Artificial Intelligence, but when I did a quick Google search on Prolog’s real world applications with the query “what can Prolog solve”, I most notably got puzzle-related results such as a Sudoku-solver. Admittedly, I could’ve worded that query better. For this assignment, I will use the same tool as the book uses: “GNU Prolog”.
The book mentions that data in Prolog is in the form of logical rules: facts, rules, queries.
A fact is a basic assertion about some world. This is the first time the book introduces the term “world”. I think another word for this could be “domain” or “context” or the likes. A rule is an inference about the facts in that world, while a query is a question about that world
Example: likes
The book starts with a basic example:
Lines 1-3 are the “facts” while line 5 is a rule. Lines 1-3 define some very simple facts such as “wallace likes cheese” or “grommit likes cheese”.
I saved this as a .pl file and then double clicked it to run it in GNU Prolog, because during the installation, GNU Prolog associated .pl files with itself. After running the file, I had the option to give my own input because I see an input cursor blinking after the “| ?- ” characters in my Prolog console.
I inputted my query as the following: “likes(wallace, cheese)” but after hitting return, all that happened is my cursor jumping to a new line. Moments later, I noticed that I was missing a period at the end of the statement. I suppose the “.” means “end of statement”, so that the user can input statements in multiple lines. Once I got the query correct, I got a “yes” as output. Changing the parameters a bit (“cheese” to “cheesea” which is supposed to be a typo) gave me a “no”. Yes and no – synonyms for true and false in the programming world.
Lines 1-3 aren’t very exciting compared to line 5. There is a lot to say about line 5 which I’ll try to keep short. According to the book, the rule is called “friend/2” which is a shorthand for “friend with 2 parameters. X and Y are the parameters in this case, while “:-” probably is Prolog’s assignment characters. Then you see three blocks divided by commas: “\+(X = Y)”, “likes(X, Z)” and “likes(Y, Z)”. The book says that X
and Y cannot be the same, which is what “\+” is for it seems.
As for the “likes”, I assume they’re like function calls which return a yes or no. When the results of these three blocks is a “yes”, then you get a “yes” as the output of “friend”. However: nowhere in the “friends” call you specify “Z”. This rule checks that if two persons like the same Z (thing), then they are friends. What Prolog does there is check every single fact with Wallace and Grommit and see if they have a matching object they like. For example, Wallace and Grommit like cheese. Therefore, “friend(wallace, grommit).” returns a “yes”. You don’t specify “cheese” anywhere, Prolog “just knows” that they both like cheese.
For the sake of experimentation, I changed line 5 to “friend(X, Y) :- (X = Y)” This should mean that a person is a friend with itself. When I called this as “friend(wallace, wallace).”, I got a “yes”. This confirmed to me that a negation indeed is written as a “\+”.
Interestingly enough, the code example can be visualized as a tree of some sorts:
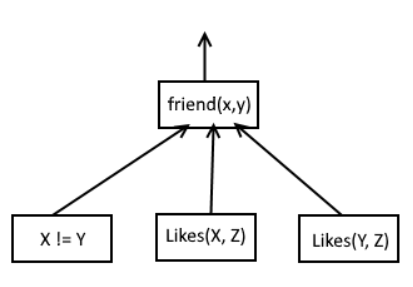
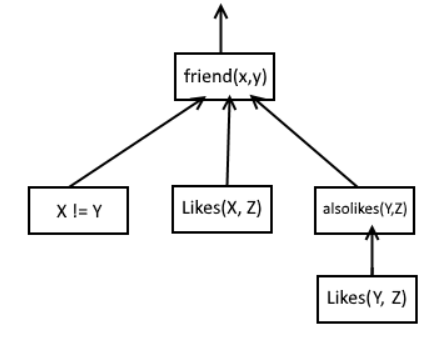
Where an arrow out is the output. And if at some point one of the arrows contains “no”, then the block the arrow is pointing at would also output a “no”. I imagine this can go infinitely deep. To test this I changed the example a bit, which also could be represented with the following tree.
Example: food
The book proceeds to a second example related to food:
A food has a type, and a food has a flavor. You find out if the food has a given flavor by querying for: the food, and the flavor. What the function does is check if a given food’s type and a given flavor’s type match up.
The book introduces a new keyword: “What”, then proceeds to call the fact as following: “food_type(What, meat).” which returns a prompt from the console: “What = spam ?”. From this point on, I can press ; to go to the next alternative, or a to list all alternatives. Prolog is telling me that spam is meat, but that there are more. When I hit ; I see “sausage”. But this is all executed in a fact. What about a rule, in this case, “food_flavor”?
When I call “food_flavor(What, sweet).”, I’m essentially asking “what food is sweet?” Then I get the following results: “jolt” and “twinkie”. This is actually pretty interesting because Prolog finds out if a food is sweet by looking at the given flavor, then searches the given flavor by matching a flavor’s food type with the food in food_type.
I like how this wildcard-like variable is called “What” because you can almost make it a humanly readable inquiry: What food has a sweet food flavor?
Example: Map coloring
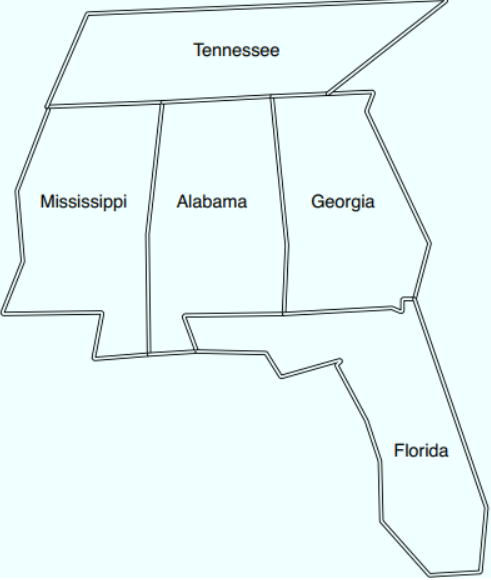
The idea is that there are 3 colors: red, green and blue. Each state has a color but adjacent states may not have the same colors touching each other. So for example, Mississippi and Tennessee may not have the same color, or Alabama may not have the same color as its surrounding states. First all color combinations are defined in “different” as a fact. Same color combinations are not allowed. Calling this code: “coloring(Alabama, Mississippi, Georgia, Tennessee, Florida).” produces the following output:
Alabama = blue
Florida = green
Georgia = red
Mississippi = red
Tennessee = green ? ;
And 5 more combinations. The fact that it managed to find color combinations without any algorithm is something I have a hard time wrapping my mind around. All this code does is defining facts and rules and it manages to find all the alternatives. Yet I have a hard time understanding how the code really works, because the book doesn’t explain the code in-depth. Maybe I’ll figure it out later on when I have more experience.
Example: unification
This final example introduces a new character: the equals sign (“=”). In Java or C#, = is used to assign something to a variable (var x = 1). But in Prolog, it means “Find the values that make both sides match.” Calling:
“dorothy(lion, tiger, bear).” produces the following output: “yes”. But calling “dorothy(One, Two, Three).” produces:
One = lion
Three = bear
Two = tiger
I suppose to “unify” one, two and three, Prolog ‘changes’ them into lion, tiger and bear, respectively. Same with X, Y, Z in dorothy – those three get changed into lion, tiger, bear when the rule is invoked. I guess that’s what is also happening at the map coloring example. The state names get mapped to red, green, blue, hence it output [State] = [Color]. It’s actually a unification output.
If I call “dorothy(One, Two, bear).” it only outputs:
One = lion
Two = tiger
There is no bear, as it’s already “the same”.
Thoughts so far
Prolog is quite interesting so far. It is somewhat reminiscent of a database where you have a bunch of records and you can execute queries, yet something feels ‘different’ about it. I still can’t wrap my mind around the Map Coloring example. I know one way or another, unification is involved, but unfortunately the book doesn’t explain it very well. It felt like that example was there for the sake of glorifying Prolog like “look at the kind of complicated problems Prolog can solve!”.
Yet, I believe in Prolog’s power. In the self study of day 1, I added my own challenge where I find all genres a specified instrument is used in, which could be done in 2 lines of code or so.
Compared to that, here’s the C# version I quickly put together.
Quite the difference, isn’t it? In Prolog I don’t need to define data structures or tie together two structures with an algorithm. Instead of that, all I need to do is define a rule.
Recursion
The chapter starts off with a recursive ancestor function. If it wasn’t recursive, I’m sure it’d be a huge chain of function calls instead, and the length of the chain would depend on just how deep you’d like to search. I imagine it would be a pain to maintain that list.
First thing I notice here is how a rule is defined twice. How does Prolog differentiate between these two? The book mentions that ancestor/2 has two clauses. “When you have multiple clauses that make up a rule, only one of them must be true for the rule to be true.”
I think in this context, a clause simply means implementation of a rule. So there are two manners to execute a rule: a simple lookup of the father, or a recursive lookup, and once one is successfully executed, there’s no need to execute the other. The book also says: “The second clause is more complex: ancestor(X, Y) :- father(X, Z), ancestor(Z, This clause says X is an ancestor of Y if we can prove that X is the
Y).
father of Z and we can also prove that same Z is an ancestor of Y.”
“zeb” is an ancestor of “john_boy_jr”. If I call “ancestor(zeb, john_boy_jr).”, I get a true. I think what happens is, behind the scenes, it calls the first clause which returns a false, it then calls the second clause. “father(X, Z)” returns a list of descendants of zeb, in this case just john_boy_sr. This is then used in the recursive ancestor call like “ancestor(john_boy_sr, john_boy_jr).” and will start evaluating from the first clause again. This time that evaluates to true, therefore, zeb indeed is john_boy_jr’s ancestor. It feels like the first clause in this case is the base case of the recursive function.
At first, I had difficulties understanding this. But writing it out step by step like this makes more sense to me. I now know that a rule can have multiple clauses and how recursion works.
Finally, the book also mentions we can use variables in a query, such as ”
ancestor(zeb, Who).”. It immediately dawned on me that the previous day I mistook “What” for a keyword. Rather, it’s just a variable named “What” for context’s sake. In this context, the author decided to use “Who” instead because we’re talking about people. Unsurprisingly, I got the descendants of zeb, then the descendants of zeb’s descendants, and so on.
Lists and tuples
There’s not much to be said here. From what I gather by reading this book, a tuple is a list but has a fixed size and is written with (), e.g. “(1, 2, 3)”. Meanwhile lists have a pipe operator which can separate it into a “head” and “tail”:

I imagine that you can “iterate” through a list if you recursively keep splitting a list into a “head” and “tail” until you have nothing left. In fact, I did exactly that.
Which outputs:

What I find interesting about lists is that lists are like arrays, except they can be accessed in two parts: the head and tail. You don’t have that in C# for example. In C#, you could use an array index 0 for the head, but accessing the tail would require copying an array over to a new array without the head.
Challenge: Textonyms
In order to delve deeper in the language (and because the assignment requires me to), I have come up with a challenge: Write a ‘textonym finder’. Rosetta Code has a page dedicated to this, but has no code example for Prolog, which means likely nobody has attempted this in Prolog before. A perfect candidate for an original challenge. I might even submit this to Rosetta Code for fun.
Originally I had an even more complicated challenge, but it had proven to be too challenging: creating a word searching puzzle. You know, the ones where you have a list of words and a grid of letters and you have to find words in it. The way I wanted to approach this problem was as follows:
- Define the horizontal and vertical width of the grid
- Define the list of words which can be used
- Define that each word can be used only once
- Define that the words can be on a horizontal or vertical grid (not diagonal for now) in either direction
- Define that the letters of those words can somewhat cross each other
The first two points are easy but things became really blurry from the third point on already, and I had no idea on how to solve this problem.
I have come across a similar problem which was a crossword puzzle solver. Solving crossword puzzles is essentially like generating a word search puzzle, except that word search puzzles don’t have blanks.

Unfortunately I really had no idea where to start even for crossword puzzles, and a bit of searching gave me some semi-popular crossword Prolog problem where they ask you to solve a symmetrical crossword puzzle. Trying to tinker around with the solutions for that problem quickly proved to be in vain, even with the GNU Prolog manual at my side, because that manual doesn’t have any practical code usage examples whatsoever.
Thankfully, I had a backup-challenge in case the first challenge proved to be difficult: textonyms.
Textonyms
In order to find the textonym of a number, I have come up with the following steps which in theory *should* work:
- Create a database of some words: ‘test’, …
- Create a dictionary of key mappings: (a, ‘2’); (b, ‘2’), …
- Input the numbers as a string (e.g. ‘43556’ which would result in at least a ‘hello’).
- Split the numbers into a list: atom_chars(In, OutList)
- Produce every single combination of the list of numbers. For example: 43556
- maps to GDJJM, HEKKM, IFLLO, GELKO, IEJJO, etc.
- See if any of those combinations exist in the words database.
- (Optional: load the database of words from a text file)
First off, I mapped each character to a number:
Then, I defined some words:
What I want to do is basically ‘map’ some numbers to a combination of characters. GNU-Prolog has a function exactly for that: maplist. This website seems to handle mapping extensively and shows many examples. One example that caught my interest is the following:

This is exactly what I needed, because I want to iterate over a list of numbers and ‘convert every character into something‘; applying a function on each element if you will.
In order to do that, I first had to write a conversion script. Actually, no, I didn’t have to, because I already have one: keymap. I can simply call it like this: keymap(Out, ‘9’). That’ll give me every single character that belongs to the number 9. I use keymap in maplist: maplist(keymap, [‘4’, ‘3’, ‘5’, ‘5’, ‘6’], Out).

I now have generated a list of all possible characters for a certain numbers with a single line of code, although it took me three days to get this far, because I spent most of my time writing a recursive function instead. Finding that maplist page is a blessing.
Next up, I’ll need to take this output and see if they exist in the database of words. For that, I’ll need to write a function which takes a list of chars as input and either put them together as a string, or splice up the words in the words database into lists of individual characters. The former sounds easier, so I’ll go with that.
After a bit of looking around, I found a function called ‘atom_chars/2’. This can either combine or split characters to/from a string. This function is also handy in splitting the input number into a list of characters for the above function. Here’s an example of how it works both ways:

I used this function in my own function called charlist(In) in order to check if a list of characters exists in the words database:
charlist(In) :-
atom_chars(Out, In),
word(Out).
It can successfully detect whether ‘hello’ exists or doesn’t exist:

Now the tricky part: putting it all together. So far I’ve made a few building blocks, and it’s time to build something functional out of it. So far, this is what I put together:
When I call mapchars with the number combination, I don’t get quite the desiredresu lt. Calling it with ‘43556’ (correct) and ‘12345’ (incorrect) gives me a boolean result rather than the matching word:

Somehow, I need to make it display the missing words. The function returns a boolean instead of the matched word. A eureka moment filled in the final piece of the puzzle: I need to return ValidWord from ‘charlist’ all the way back to ‘mapchars’, so I changed the final two lines. This is how the function looks like now:
And the function call:
In the end, maplist saves the day! I expanded the database for entry 43556 some more with additional words:
And the result:
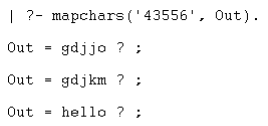
Curiously enough, GNU-Prolog is unable to tackle the first two words in the database due to environmental constraints:
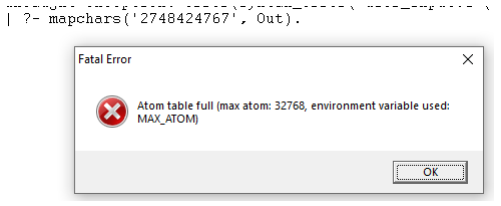
I am unable to find a solution for this, even when I search for the exact word combination “Atom table full”. Out of curiosity, I experimented to find the limits:
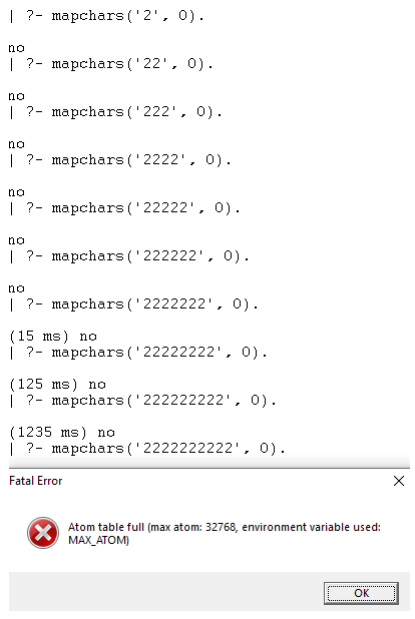
The maximum amount of characters I can query is 9. Any more than that, and the program crashes.
Words database
To go an extra mile, I wanted to populate the database of words with a text file. I found a way to read files line by line into an array, but didn’t find a way to create facts out of those words. Unfortunately, I had to leave this out of the challenge due to time constraints.
This is how the end result looks like.
Interfacing and real-world applications
Prolog is an interesting language but I find it somewhat constraining that I have to work from the GNU-Prolog program. Right now this is more of an academical context, but what if I wanted to actually use Prolog in some of my applications? For example, how do I call Prolog from C# or Java? Or what if I want to make visual applications and not just CLI? In this post I will briefly look into various options. Note that I won’t distinguish between Prolog dialects (GNU/SWI-Prolog, and so on).
C#
Yield Prolog: Not exactly a Prolog compiler in C#, but it does add a “Variable” keyword which in combination with Prolog should simulate Prolog’s unification.
Also, it seems like NuGet also has a lot of Prolog-related packages, although the amount of downloads seem to be minimal:

Java
JPL: It seems to allow for embedded Java code in Prolog, and the other way around.
B-Prolog: This also seems to have a bi-directional interface with Java but also C.
SICStus Prolog: According to this page, you can embed SICStus Prolog in Java or .NET application servers.
JavaScript
Tau Prolog: A Prolog interpreter written entirely in Javascript. This means that you can place Prolog code in Javascript files and it’ll execute. There’s also a Node.js NPM package for it.
Use cases
There are various use cases for Prolog, which I will list below.
- The Java Virtual Machine had (has?) a class verifier written in Prolog
- It’s possible to write GUIs in SWI-Prolog by using XPCE
- Searching on Google for Natural Language Processing (NLP) seems to bring up quite a good amount of results
- Here are some more use cases someone dug up
- A chunk of IBM Watson’s code is written in Prolog
Closing thoughts
Although there are quite some Prolog-related content on the internet from communities, most of them seem to be tutorials or people asking questions. Some websites I come across also look like they’ve been written pre-2005. I have the feeling that nowadays Prolog is applied more in an academic context rather than modern-day applications and is slowly fading into obscurity.
One major annoyance I had with Prolog is how there are dialects (GNU/SWI) and how they seem to differ a bit in functionality. SWI Prolog shows up in searches more often so it makes me wonder why the Seven Languages in Seven Days book decided to go for GNU Prolog. There also doesn’t seem to be any official IDE for Prolog and debugging Prolog code is something I can only dream of .
It also feels like (at least GNU) Prolog is tailored for older machines, which I noticed when I tried to generate textonyms for more than nine numbers. Some websites also have ancient designs which kind of gives me the impression that Prolog is an ‘ancient’ language probably used in legacy systems nowadays.
Besides the annoyances, I found Prolog itself to be quite interesting, especially with unification being able to go both ways. For example, atom_chars can split an atom into chars, or merge chars into an atom. Normally in C# you’d have two separate functions for that. In Prolog you just define a variable and Prolog fills it in for you. That’s what my textonym-program mainly uses too. Although the opposite doesn’t
seem to be possible (finding numbers for a word) because of the way I used atom_chars.
Truthfully, I just can’t help but have mixed feelings about Prolog as a language. Logical programming as a concept, however, is most interesting.